
LOGINV: Returns the value of the inverse log-normal cumulative distribution with given mean and standard deviation at a specified value.ĮXPONDIST: Returns the value of the exponential distribution function with a specified lambda at a specified value.īINOMDIST: Calculates the probability of drawing a certain number of successes (or a maximum number of successes) in a certain number of tries given a population of a certain size containing a certain number of successes, with replacement of draws. LOGNORMDIST: Returns the value of the log-normal cumulative distribution with given mean and standard deviation at a specified value. NEGBINOMDIST: Calculates the probability of drawing a certain number of failures before a certain number of successes given a probability of success in independent trials. NORMINV: Returns the value of the inverse normal distribution function for a specified value, mean, and standard deviation. NORMSDIST: Returns the value of the standard normal cumulative distribution function for a specified value. NORMSINV: Returns the value of the inverse standard normal distribution function for a specified value. POISSON: Returns the value of the Poisson distribution function (or Poisson cumulative distribution function) for a specified value and mean. WEIBULL: Returns the value of the Weibull distribution function (or Weibull cumulative distribution function) for a specified shape and scale. ZTEST: Returns the one-tailed P-value of a Z-test with standard distribution. Standard_deviation - The standard deviation (sigma) of the normal distribution function.Ĭumulative - Whether to use the normal cumulative distribution function rather than the distribution function.
Mean - The mean (mu) of the normal distribution function. X - The input to the normal distribution function. NORMDIST(x, mean, standard_deviation, cumulative) Given a discrete random variable X, and its probability distribution function P ( X x) f ( x), we define its cumulative distribution function, CDF, as: F ( x) P ( X k) Where: P ( X x) t x min x P ( X t) This function allows us to calculate the probability that the discrete random variable is less than or equal to some. The operation which combines the two functions $f_X$ and $f_Y$ in this fashion isĬalled convolution.The NORMDIST function returns the value of the normal distribution function (or normal cumulative distribution function) for a specified value, mean, and standard deviation. Marginal functions occur midway through the proof.Į(X + Y) &= \sum\limits_x \sum\limits_y (x+y) P_x$ Then to find the expectation you need to find. and in reverse F ( x) 1 x f ( t) d t for x 1.
#How to find cdf how to
Observations are that the order of the summations (or integrals) can be swapped, and that If you have the cdf then you want the anti-integral or derivative which with a continuous distribution like this. How to find a cumulative distribution function from a probability density function, examples where there is only one function for the pdf and where there is. The proof, for both the discrete and continuous cases, is rather straightforward. Will be equal to the sum of their expected values. The cumulative distribution function (CDF) of 2 is the probability that the next roll will take a value less than or equal to 2 and is equal to 33.33 as there. Expected Valueįor any two random variables $X$ and $Y$, the expected value of the sum of those variables
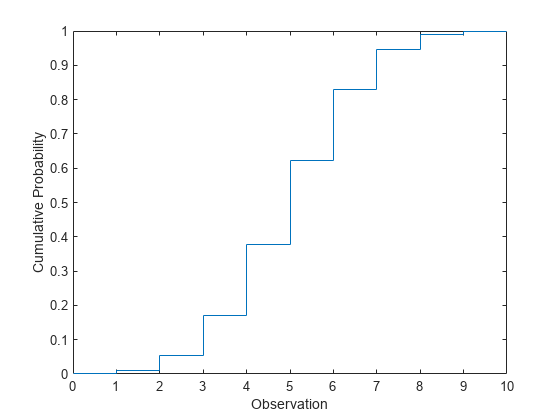

F (n) n 0 0.25xdx 0.25x2 2 n 0 0.25n2 0.25(02) 2 0.125n2, where 0 n 8 F ( n) 0 n 0.25 x d x 0.25 x 2 2 0 n 0.25 n 2 0.25 ( 0 2) 2 0.125 n 2, where 0. To calculate the Cumulative Density Function (CDF) for a normal random variable at a value x, also writen as F(x), you can transform your distribution to. The CDF is the integral of the PDF and in this case is. Therefore, we need some results about the properties of sums of random variables. Well we already kind of did that when checking if the area under the curve equals one.
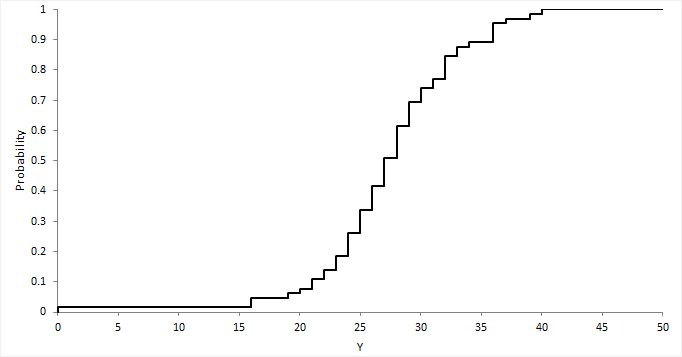
The most important of these situations is the estimation of a population mean fromĪ sample mean. Many situations arise where a random variable can be defined in terms of the sum of other random


 0 kommentar(er)
0 kommentar(er)
